FFTアナライザの基礎と概要 (第2回)
<連載記事一覧>
第1回:「はじめに」「FFTアナライザが登場する前にあった周波数分析器」「FFTアナライザ」「FFTアナライザを選定するための仕様の理解」「【コラム】FFTアナライザとよく似た測定器との違い」
第2回:「FFTアナライザの構造」「窓(ウィンドウ)関数の使い方」「アベレージング(平均化処理)」「FFTアナライザに接続されるセンサ」「【コラム】日本国内で販売されているFFTアナライザ」
第3回:「FFTアナライザの測定事例」「FFTアナライザの校正」「おわりに」「【インタビュー】小野測器のFFTアナライザ事業への取り組み」
FFTアナライザの構造
FFTアナライザの基本的な構造は入力回路、A/D変換器、絶縁回路、デジタル信号処理回路、制御回路、ディスプレイ、スイッチパネル、電源となっている。初期のFFTアナライザのA/D変換器は8~12ビットで、デジタル信号処理回路はミニコンピュータかマイクロプロセッサであった。最近のFFTアナライザの多くには24ビットA/D変換器が搭載され、デジタル信号処理回路は高速DSP(Digital Signal Processor)となっている。
図16. 最近のポータブル型FFTアナライザのブロック図(小野測器、CF-9200)
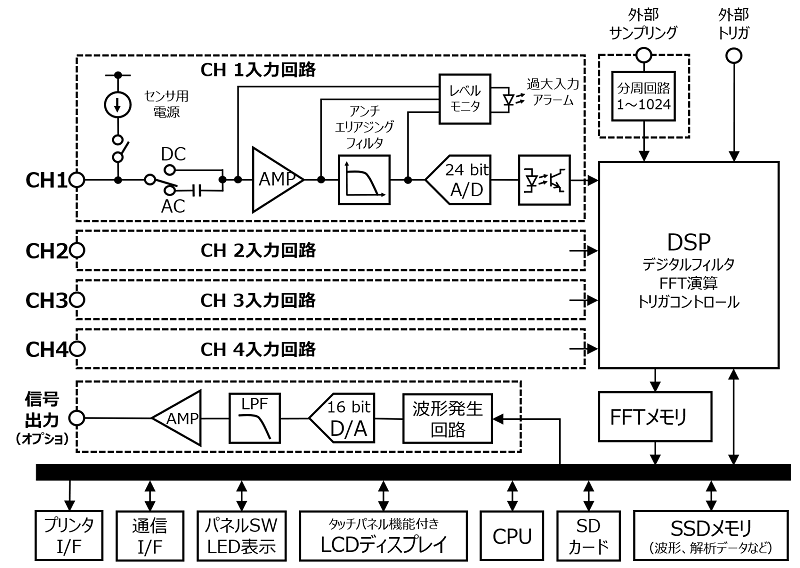
FFTアナライザにはポータブル型とPCベース型がある。PCベース型ではFFTアナライザの設定、測定結果の表示、測定結果の保存はパソコン側で行うため本体には入力端子と通信ポートなどが最小限の端子しかない。
窓(ウィンドウ)関数の使い方
FFTアナライザは現象の一部を切り取って、その現象から得られた観測信号が繰り返すという仮定で周波数分析を行う。そのため信号の両端に現れる不連続の影響が周波数分析結果に影響する。
図17. 窓関数を使わない場合の問題点
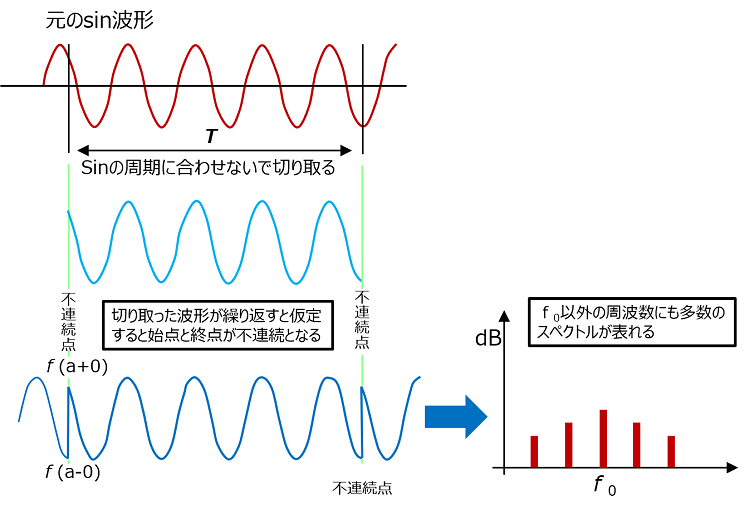
この問題を避けるため、切り取った現象の両端を窓関数によって加工して不連続の影響を少なくする工夫がされる。
図18. 窓関数の効果
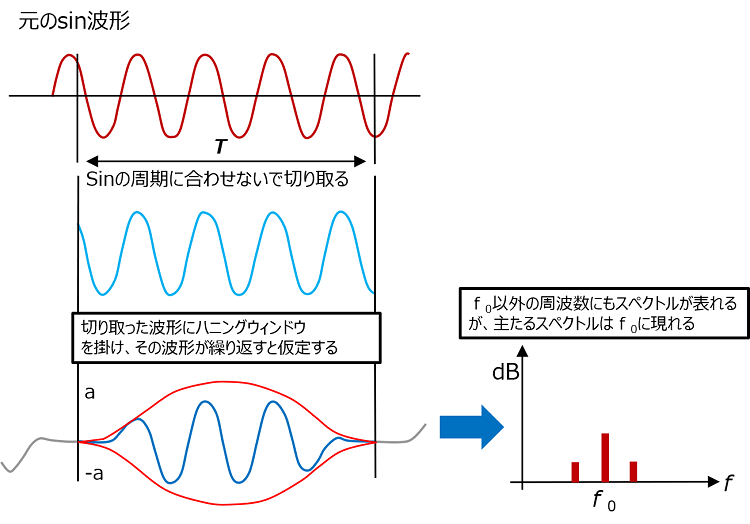
窓関数の種類と特長
窓関数はさまざまな形が考案されたが、ここではよく使われる3種類について紹介する。
図19. 主な窓関数
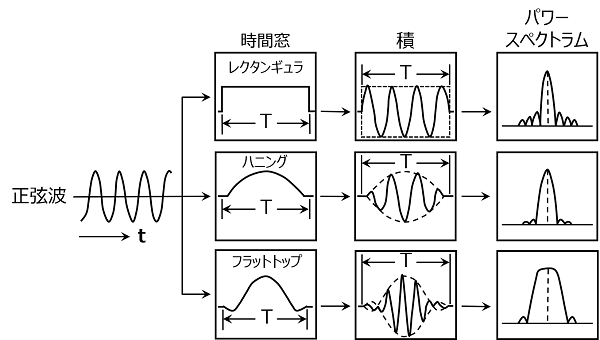
実際に音響や振動の測定では測定の目的によって窓関数を切り替えて使う。窓関数の設定によって測定結果の見え方が異なるので注意が必要となる。
| 種類 | 周波数 分解能 |
用途 |
|---|---|---|
| レクタンギュラ | 良い | インパルス波形などの過渡信号 |
| ハニング | 普通 | 一般の連続信号 |
| フラットトップ | 悪い | 高周波分析などレベルを重視する信号 |
アベレージング(平均化処理)
FFTアナライザに搭載されたアベレージング機能を使うことによってノイズに埋もれた信号の観測や、ばらつきの大きな測定などではアベレージングを行うことによって現象の特長が見えやすくなる場合がある。
周波数アベレージング
FFTアナライザによって得られた周波数ごとの信号の強度が得られる。得られた周波数ごとの信号強度を平均化することによってノイズによるスペクトルが平坦化され、観測したい信号に含まれる周波数成分が見えるようになる。
周波数アベレージングには位相情報を含むフーリエスペクトル平均と位相情報を含まないパワースペクトル平均がある。
アベレージングには加算平均と指数平均がある。加算平均では指定された回数の平均が終わると測定結果が表示される。指数平均では最新のデータへの重み付け係数を掛けて平均化しているため、平均化処理を止めない限り、無限に平均化処理を繰り返す。
時間軸アベレージング
デジタルオシロスコープやメモリレコーダに搭載されているアベレージング機能と同じである。ランダムノイズに埋もれた信号を観測する場合は、固定したトリガ点を決めて同じ信号を繰り返し観測して平均化を行えばランダムノイズの影響は軽減される。また平均化することによって振幅分解能が上がる。
時間軸アベレージングされた測定結果をFFTすることによってダイナミックレンジの大きな測定結果が得られる。ただしこの機能が有効となるのは安定した繰り返し現象のみで、単発の現象はアベレージングができない。
アベレージングには指定された回数の平均化処理が終わる加算平均と平均化処理を止めない限り、無制限に平均化処理を繰り返す指数平均がある。

pc.png)
