計測・測定の基礎 | 周波数を解析する
オシロスコープなどの波形観測用測定器は、時間とともに変化する「波形」を捉えます。時間軸のデータはフーリエ変換により周波数軸に変換できます。
図1. 時間軸波形の周波数軸での観測
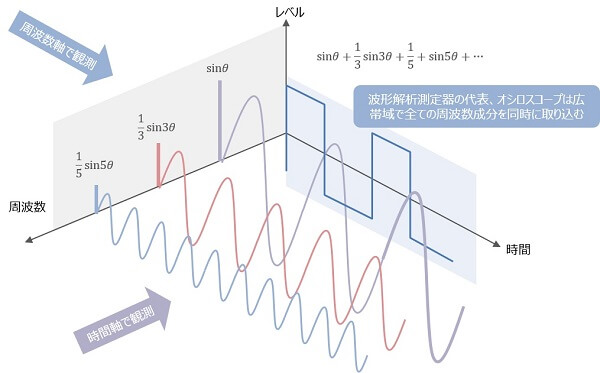
高速フーリエ変換(FFT)により波形の周波数成分の解析を行える測定器がFFTアナライザです。DC~100kHz程度までの周波数をカバーできます。FFTでは有限の時間軸データの最初と最後をつなぎ合わせて、無限の繰返しデータとみなして解析します。そのため最初と最後に段差があるとエラーの原因になるため、両端のウェイトをゼロとするような窓関数を掛算して最初と最後のデータをそろえます。
図2. 有限の時間軸データと窓関数
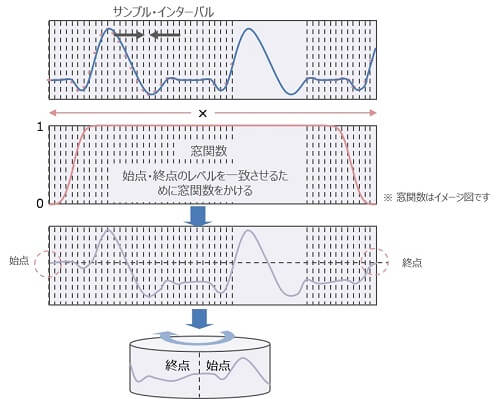
窓関数は、よく使用されているハニングやフラットトップなど、複数が用意されています。波形によって最適な窓関数を選択します。FFTにより「周波数VS振幅」、「周波数VS位相」のデータが得られます。
アナログ信号をデジタル・データに変換する際に必ず守らねばならない決まり事が「標本化サンプリング定理」です。原信号に含まれる周波数成分をすべて正確にサンプリングするためには、最高周波数成分の2倍以上のサンプリング周波数が必要です。
サンプリング周波数(計測器の世界ではサンプル・レートということも多く、その場合は○○S/s・・・サンプル/秒を使う)の半分の周波数をナイキスト周波数と呼び、これを超える信号成分はあってはなりません。
図3. 標本化定理と計測器(サンプル・レートと周波数帯域の関係)
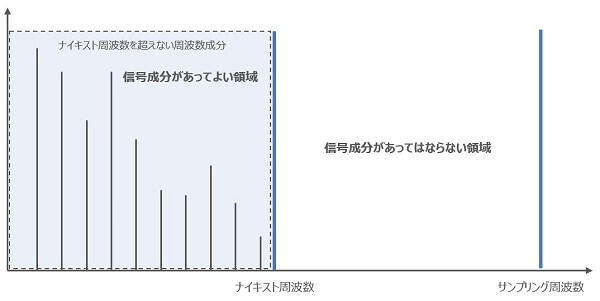
例えばコンパクトディスクの規格ではサンプリング周波数は44.1kHzとなっています。これは可聴周波数といわれる20~20kHzをカバーするためです。もしも標本化定理に違反したらどうなるのでしょうか?
図4は周波数成分が50MHz未満の信号を100MHzでサンプリングした場合です。折り返し誤差は50MHz以下には現れません。
図4. 標本化定理に違反しない場合
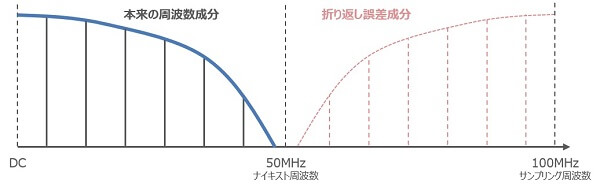
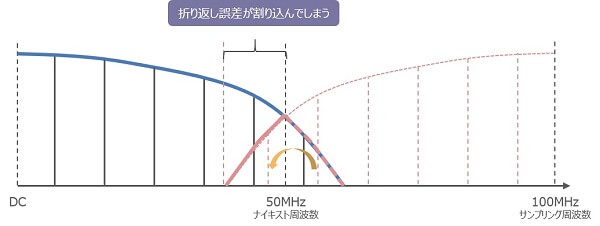
もしも50MHz以上の周波数成分が存在すると、ナイキスト周波数で折り返されてしまいます。本来は無い周波数成分が誤差として含まれてしまいます。
図5. 標本化定理に違反した場合
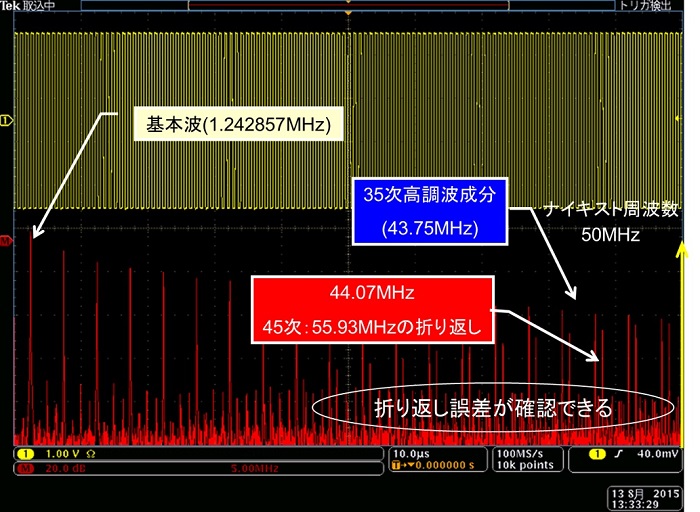
周波数1.242857MHz、立ち上がり時間2nsのクロックを100MS/s(ナイキスト周波数は50MHz)で取り込み、FFT処理した例です。横軸左がDC、右端が50MHzです。ほとんどは奇数次高調波ですが、高周波側には高次高調波だけでなく、折り返し誤差も含まれていることがわかります。
図6. 立上り時間10ns@サンプルレート100MS/s
他の基礎コラムはこちらから

pc.png)
